# Mathematics
# Encryption
This chapter is dedicated to demystifying what can seem as overtly complicated. We will try to simplify down the way specific types of encryption work at a fundamental level to help better understand what is actually going on.
# Understanding RSA
### Setting the Stage
I want this paper and exercise to be fun and enlightening for everyone.
I will try to make it fun and easy to follow along without glossing over too much of the underlying maths.
That being said, if this is not for you, or you just hate math, I encourage you to still try.
I will be adding python code blocks you can run as we move through the paper which I hope will make it more interactive and engaging.
### So what is RSA?
We can't start talking about what RSA is without first paying homage to the creators, where it gets its name.
Ron Rivest, Adi Shamir, and Leonard Adleman collaborated and invented this public key system back in 1977, which in of itself really
does show its stability since it is still used widely today. RSA as I said before is a public key system or also known as an
Asymmetric encryption. This basically means that the encryption key is actually made public for everyone to use, called a public keys
then a 2nd decryption key us held privately by the owner, simply named a private key.
But I am sure many of you know this and thats not why you are here, you are here for the Juicy bits
### Defining the Language
As with most mathematics, someone a while ago decided to use fancy letters to represent things, probably as a way to flex their
intelligence... I'm joking for the most part, normally this is done to help differentiate between different types of mathematics.
I plan on doing some First order Logic papers eventually and you will see what I mean by that then.
ANYWAY... Lets just make a table we can refer back to later to help.
|Symbol|Meaning|Do we Keep it Private?|
|---|---|---|
|p| Prime #1 | TRUE |
|q| Prime #2 | TRUE |
|n| n = p * q | FALSE |
|φ(n)| φ(n) = (p-1) * (p-1) | TRUE |
|e | pick any integer where 1 < e < φ(n) AND e is a coprime of (n AND φ(n))| FALSE |
|d | where d*e(mod φ(n)) = 1 | TRUE|
Now, I will gloss over the phi function here but if you want to learn more as to where it comes from there are links at the bottom
e and d (for encryption and decryption) on the other hand needs some explaining but hang with me we have some tricks.
The first part of e is simple enough, we need a integer that is between 1 and φ(n) which at this point we know. The second part however,
what does coprime mean, well in this case it means it shares no common factors with both n and φ(n). Now what we can do to simplify this
is to just say e must be prime, and not a divisor of φ(n) (or if you divide φ(n) by e you do not get a whole number),
which we can do some quick checks to be sure.
For d what we need to find a value that results in multiplying it by e and then doing mod φ(n) which gives us 1. I will go into how to find
this in our first example.
To clear the air incase anyone is rusty or does not know what 'mod' means it basically is a remainder function, you shove
a number into a mod(n) and you get out what is left over. I like to picture it like a clock which is mod(12). So if you know
military time you kind of do this already, 1400 hours is actually 14 mod(12) which is 2, or 2pm. You count up to 12 and then
start back over so 5 mod(3) would be 2, and 12 mod(5) would be 2 like 1,2,3,4,5,1,2,3,4,5,1,2
### Example Please...
OK you stuck with me this long lets generate some keys. For this first one we will start with really small prime numbers.
Clearly this is a terrible idea since the smaller our starting primes are the easier it is to crack, but the math is still the same
and it is faster and easier to follow along.
1. Pick 2 primes, our p and q, let's say 67 and 79
2. Generate n by multiplying p and q to get 5293
3. Generate φ(n) by multiplying p-1 and q-1 to get 5148
4. For e, pick a prime number between 1 and 5148 and is not a divisor of 5148, let's go with 17
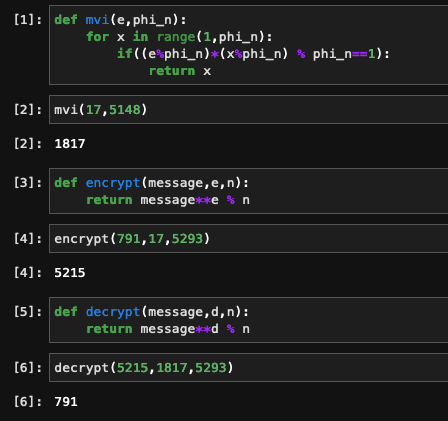
5. For d we find a value where d*e(mod φ(n)) = 1, lets go with 1817
OK, now you might be asking, how the hell did I get 1817 for d, the question feels kind of brute forced. Well this is where
I used the first bit of python code we really kind of need.
```py
def mvi(e,phi_n):
for x in range(1,phi_n):
if((e%phi_n)*(x%phi_n) % phi_n==1):
return x
```
I called this mvi which is short for Modular Multiplicative Inverse, which I will also kind of gloss over as well,
but I wanted you to see that you don't need to manually guess and check by hand, this does it for you.
So now we have our numbers, let't table them back out
|Symbol|Value|
|---|---|
|p| 67 |
|q| 79 |
|n| 5293 |
|φ(n)| 5148 |
|e | 17 |
|d | 1817 |
### Great now what...
Well now the fun starts, again we are kind of doing this by hand so rather than starting with a string and converting it
to a number to encrypt then send and then decrypt then convert back into a string lets just encrypt a number using our
new keys
First we need to send our Pub key to Alice, this is the pair of numbers e and n, so we will send her (17, 5293).
Again this is public, so we can send this however we like, as long as we are sure its not messed with on the way.
Now Alice will send us a secret number by encrypting a clear number using this public key and that is done with the
following function
NOTE: For those that do not know, the power function in python (pow()) allows for 3 inputs with the 3rd being Mod which comes in really handy for us since it is way more effienent than doing `message**e % n`
```
def encrypt(message,e,n):
return pow(message,e,n)
```
Thats it, so in this case let's send 791, so we do `encrypt(791,17,5293)` which results in 5215
Bob gets 5215 and needs to decrypt it and that is done with this function
```
def decrypt(message,d,n):
return pow(message,d,n)
```
This is almost the same but we swap out the e for the d, and if we plug in `decrypt(5215,1817,5293)` we get, you guessed it, 791
And to show Im not making this up...
[](https://docs.hackliberty.org/uploads/images/gallery/2022-05/TqDpiF2ceumYtBO2-python.png)
The last bit is a full python function you can play with to do some encrypton and decryption using what I have shown
```py
def simple_rsa_gen():
# Just a short list of 3 digit primes we can pick from so you dont need to find your own
primes = [211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379]
# Lets pick our p and q from this list
p = primes[(randint(1,29)-1)]
q = primes[(randint(1,29)-1)]
# Lets make sure we did not happen to pick the same prime for both
if p == q:
while p == q:
q = primes[(randint(1,29)-1)]
print("p = "+str(p))
print("q = "+str(q))
# Now lets generate n by getting the product
n = p * q
print("n = "+str(n))
# Lets get that phi_n we need
phi_n = (p-1)*(q-1)
print("phi_n = "+str(phi_n))
# Lets find a good value for e, remember this needs to be a prime between 1 and phi_n and cannot be a divisor of phi_n
# you will see my range is not going to start at 1, first becuase 1 is not prime also I want to move into 3 digits to start
def get_e(var_phi_n):
for i in range(101, var_phi_n):
prime = 1
for j in range(2, i // 2 + 1):
if (i % j == 0):
prime = 0
break
if (prime == 1):
if var_phi_n % i != 0:
return i
break
# So let me break down what I just did, first we need to pass in what out phi_n is, that will be out upper limit
# then we need to determine if its a prime which we can do by seeing if its mod returns 0 for any int up to itself
# which in laymans terms means does it have any devisors at all, then if it is a prime we just make sure it't not
# a divisor of phi_n which just can be checked with does phi_n mod n = 0, if it does its no good
# Now we are starting at 101 and in most cases this will work for us, would be rare to find an instance where 101
# is infact a divisor of your phi_n so expect to see it more times than not. In general the goto e is actually 2^16 + 1 = 65537
e = get_e(phi_n)
print("e = "+str(e))
# Lets get that d value we need, the bigger phi_n gets the longer this could take
# here we are doing that mvi funtion again and the larger your starting primes the longer this can take
def mvi(var_e,var_phi_n):
for x in range(1,phi_n):
if((var_e%var_phi_n)*(x%var_phi_n) % var_phi_n==1):
return x
d = mvi(e, phi_n)
print("d = "+str(d))
# Now we have all of he numbers we need. Lets make our pub and priv keys and end this.
print("Your Public key is ("+str(e)+","+str(n)+")")
print("Your Private key is ("+str(d)+","+str(n)+")")
# Now we can use these with the encrypt and decrypt functions we made before
```
The output from above will look something like this
```
p = 283
q = 211
n = 59713
phi_n = 59220
e = 101
d = 57461
Your Public key is (101,59713)
Your Private key is (57461,59713)
```
And then you can use them to run those functions we defined before
[](https://docs.hackliberty.org/uploads/images/gallery/2022-05/q7YOjVDrTov5Cuw6-encdec.png)
### Is this real life?
For the most part yes, of course it is. The big differences are when actually implemented in code there are some better
methods for being more efferent as well as using random primes that are hundred of digits long, not 2.
For example, try the above code and method with 2 much bigger Mersenne primes 2^521 - 1 and 2^607 -1
You can see this in practice in the openssl sourcecode for rsa generation here.
[OpenSSL rsa_gen.c](https://github.com/openssl/openssl/blob/master/crypto/rsa/rsa_gen.c)
Look around line 174 and go from there, see if you can gather what its doing and how it is being more efficient than what we did.
### So you seen some stuff
This was a very high level and I did for sure gloss over some things but the math is there and I encourage you to look at
what I have shown here and ask yourself some questions, challenge yourself
1. Can you see any potential issues, how would you get past them?
2. Can you update the functions to use strings not just numbers?
3. In our first example what happens if I picked the number 31337 like we did in the 2nd example?
If you liked this please let me know back in the community post where I linked this, if you have questions or want more
let me know that too.
### More Links
I said I would
- https://en.wikipedia.org/wiki/RSA_(cryptosystem)
- https://en.wikipedia.org/wiki/Modular_multiplicative_inverse
- https://yewtu.be/watch?v=-ShwJqAalOk
- https://yewtu.be/watch?v=JD72Ry60eP4
- https://yewtu.be/watch?v=S9JGmA5_unY
- https://yewtu.be/watch?v=O4xNJsjtN6E
### A Little More
When I changed to pow(message,d,n) I was able to do bigger primes much faster so I put together another one using 5 digit primes you can play with.
```py
def bigger_rsa_gen():
# Doing a bit Bigger list of 5 digit primes now
# I stripped comments to save space
primes = [17029,17033,17041,17047,17053,17077,17093,17099,17107,17117,17683,17707,17713,17729,17737,17747,17749,17761,18233,18251,18253,18257,18269,18287,18289,18301,18307,18311,18313,18329,18341,18353,18367,19207,19211,19213,19219,19231,19237,19249,19259,19267,19273,19289,19301,19309,19319,19333,19373]
p = primes[(randint(1,49)-1)]
q = primes[(randint(1,49)-1)]
if p == q:
while p == q:
q = primes[(randint(1,49)-1)]
print("p = "+str(p))
print("q = "+str(q))
n = p * q
print("n = "+str(n))
phi_n = (p-1)*(q-1)
print("phi_n = "+str(phi_n))
def get_e(var_phi_n):
for i in range(10007, var_phi_n):
prime = 1
for j in range(2, i // 2 + 1):
if (i % j == 0):
prime = 0
break
if (prime == 1):
if var_phi_n % i != 0:
return i
break
e = get_e(phi_n)
print("e = "+str(e))
def mvi(var_e,var_phi_n):
for x in range(1,phi_n):
if((var_e%var_phi_n)*(x%var_phi_n) % var_phi_n==1):
return x
d = mvi(e, phi_n)
print("d = "+str(d))
print("Your Public key is ("+str(e)+","+str(n)+")")
print("Your Private key is ("+str(d)+","+str(n)+")")
```
# Theory
This chapter is dedicated to mathematical theory such as Set Theory, Type Theory, Logic and alike
# First Order Logic
### Before we Start
To be frank, this is kind of an off the wall paper. First order logic is not something you would normally
come across unless you are doing rather advanced mathematics or AI theory. I have always been fascinated by it
and ever since I learned it I feel that my problem solving and deduction skills have improved greatly. I will
also admit I do not expect many people to actually read all of this and take away everything, it is a complicated
topic and I plan on only scratching the surface. My hope really is to just plant a seed, and if you are someone
who lets the seed grow and runs with it then thats great, if not thats fine. I will have fun writing this paper
none the less.
### What is First Order Logic (FoL)
In short, it's a refined and strict language that allows you to write logical formulas that allows for both quantifiers and predicates. Already this may seem like a lot but we can break this down. By strict language I specifically mean that it has very strict rules. The syntax is either correct or it is not, down to a computer being able to determine if it is well formed easily. Quantifiers are just ways of saying the scope some given set, and there really are only 2, either ALL OF or AT LEAST ONE OF. I will get into examples of that next. Predicates can be thought of as functions, it takes in a variable and returns a value. Most of the time when you look at simple FoL you will see examples where the predicate is logical, there is no defined function, but rather the word used as the function is the definition. For example round(ball) would be true vs round(square) is false. We don't need to define the function for round() since the reader knows what that means. Now you can define predicates if you wish, that is up to you.
### What does the language look like?
The language can get very messy if you are not prepared for it, and I find a lot of papers and wikis on FoL gloss over the symbols before just shoving formulas down your neck. So lets table out the main ones we will be working with
#### Quantifiers
|Symbol | Formal Name | Meaning |
|--:|:---------------------------|:-----------|
| `∀` | universal quantification |For All of |
| `∃` | existential quantification |There exists|
The upside down A and backwards E really are very simple once you get past the fact that they are very abnormal characters. Simply put the `∀` just means that all values it's referring to are considered where as with `∃` only 1 needs to be taken into account. A good example would be `∀food tastes good` vs `∃food tastes good`, which is like saying "All food tastes good" verses "Some food tastes good". In the first we are saying all food must taste good for the statement to be true and in the second technically we are saying that only one food needs to taste good for it to be true.
I do want to call out 1 more, we will not be using it but it does exist and it is `∃!` which just means "there exists 1 and only 1". Sticking with our last example of food you could assume a really picky child would say `∃!food tastes good` and they could be referring to like chocolate or something. Not the best example but you get the point.
#### Predicates
Predicates are evaluations we make to objects. As I stated before, and for this paper, we will stick to using words that already have meaning to be our predicates. Using our last example we can just turn `tastes good` into a predicate by treating it like a function, for example `∀food goodTaste(food)` vs `∃food goodTaste(food)`. Now we can start to look at this as a computable test in that for the `∀` we could loop through all foods and if we find a single one where goodTaste(food) returns false it is then false where as with `∃` we could loop through all food and if a single one returns true for the same function then the statement is true.
#### Logical Connectives
This is the first time I brought these up but they are used in every language from speech to computers. They are your ANDs, ORs, and NOTs for the most part. Since this is a well defined language they had to make it fun and use their own symbols for Everything so lets table them out
|Symbol | Meaning |
|--:|------------|
| `¬` | NOT |
| `∧` | AND|
| `∨` | OR |
There are more and you can see them [here](https://en.wikipedia.org/wiki/List_of_logic_symbols) but for what we will be doing these are all we need.
#### Some extra symbols
I plan on doing a whole paper on set theory as well some day, but basically it is the study of sets and it also has its own set of symbols. I will be using one main one from this language to help clear up what a specific variable is representing which is the "set membership" symbol of `∈`. A quick way to see this in action would be with small sets of integers. `1 ∈ {1,2,3}` would be true where as `4 ∈ {1,2,3}` would be false. I could also say things like `4 ∈ positiveIntegers` which would then be true. If you are interested you can see a list of symbols [here](https://www.rapidtables.com/math/symbols/Set_Symbols.html)
### Ok so now what?
Well now that we have some clarification we can start to play a bit and really my favorite is the "beetles and bugs" saying, "All beetles are bugs but not all bugs are beetles". As an adult its kind of trivial but we can use this as a simple example to write some functions. Let's break it down
1. All Beetles are Bugs
- so we can write this as
- `∀beetles ∈ bugs`
2. Not All Bugs are Beetles
- And we can write this as
- `¬∀bugs ∈ beetles`
Now we can mix things around and try to ensure the statement is true. For example if `¬∀bugs ∈ beetles` is true then is `¬∃bugs ∈ beetles` true? No, because there are some bugs that are beetles, so the statements `∀beetles ∈ bugs` and `∃bugs ∈ beetles` are both true. Before we move on I am going to rewrite these in a little different way so it lines up with our next examples. `∀beetles ∈ bugs` can be rewritten like this `∀x bug(x), x ∈ set of all beetles`, and `∃bugs ∈ beetles` can be rewritten as `∃x beetle(x), x ∈ set of all bugs`. So what did here was gave a predicate for beetle and bug, basically a function that will determine if the object satisfies the condition of being one or the other. We can say these in a sentence like this `∀x bug(x), x ∈ set of all beetles` "For all of x, x is satisfied by the predicate bug(), where x is a member of the set of all beetles". Where as `∃x beetle(x), x ∈ set of all bugs` would be "There exists an x that is satisfied by the predicate beetle(), where x is a member of the set of all bugs".
### How about a mental challenge
Now that you have a taste and know whats being said with the language let's try a simple challenge.
- Given the statements below, which are true
1. `∀x ∃y (x + y = 10), x, y ∈ Positive Integers`
2. `∀x ∃y (x + y = 10), x, y ∈ Integers`
3. `∃x ∃y (x + y = 10), x, y ∈ Positive Integers`
4. `∀x ¬∃y (x + y = 0), x, y ∈ Positive Integers`
In these examples we do not define a predicate name since it is itself a function `x + y = 10` in that you can plug numbers into it and check. See if you can figure these out on your own before moving on.
Click to see Answers
Now I did throw a curveballs at you here, being that I put 2 quantifiers with 2 variables rather than 1, but when you read it out loud you basically just say AND between the 2
1. `∀x ∃y (x + y = 10), x, y ∈ Positive Integers`
- False
- In this case we are saying, for all of x there exists a y where x + y = 10, where x and y belong to the set of all positive integers. Reading it this way does it come off more logically?
- Why is it false?
- We can plug in a value for x where there is not a single y that could make it true, specifically if "x > 9". If x was 10 then y would have to be 0 and if x was 11 y would have to be -1 and neither of those are part of the set of all Positive Integers.
2. `∀x ∃y (x + y = 10), x, y ∈ Integers`
- True
- Why is it True?
- This one on the other hand is the same BUT we expand our domain out to all integers which would include 0 and negative numbers so now we can find an y for every x. If x was 30, we could put y as -20, if x was -90 we could put 100 for y
3. `∃x ∃y (x + y = 10), x, y ∈ Positive Integers`
- True
- Why is this True?
- Now this one has 2 `∃` quantifiers which basically tells us that we really only need to find 1 example thats true. We can put 5 for x and 5 for y and boom, mic drop, walk away
4. `∀x ¬∃y (x + y = 0), x, y ∈ Positive Integers`
- True
- Why is this True?
- In this one we added a NOT to the 2nd quantifier and the function changed a little, reading it in english it would be "For all of x there is not a single y that makes x + y = 0 true if x and y are positive integers" and with a little reasoning we can conclude this is a true statement. If we switched the domain to Integers then this statement would be false since we would actually have an infinite number of combinations we could come up with to have x + y = 0, {(0,0), (1,-1), (2,-2), ...}
### What is the Takeaway?
If you stuck with me this far that's awesome and really the takeaway is just a new language you can use to refine your deductive reasoning. Basically any statement can be rewritten in FoL and you can use that to really dig into the statement and learn if it's true or not. Or perhaps you need to define more variables or your predicates need to be defined better. I personally have found it rather rewarding boiling statements down into FoL to really get to an answer, but also Im weird...
Again I have only scratched the surface here, this is a massive and complicated topic and sadly the doorway to it is also complicated and rather esoteric, but based on what you have learned can you understand what my bio line from Lemmy is now?
If you have any questions or want to learn more you can reach me in matrix `@ackermann:hackliberty.org`